Editor's Pick
-
Andy
-
Andy
-
Andy
-
Andy
-
Andy
-
aplesch
-
Andy
-
Andy
-
Andy
-
aplesch
-
Andy
-
Andy
-
Andy
-
Andy
-
Andy
-
Andy
-
Andy
-
crystal h
-
Andy
-
advercis
-
Luke Messenger
-
Andy
-
Andy
-
Andy
-
Andy
-
Andy
-
Knoblauch
-
Andy
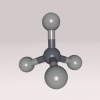
- This is my first and simple construction of a molecule. I chose to do Methane (CH4), one atom of carbon and four atoms of hydrogen, because it takes the shape of a tetrahedron. In this blog, I used a different...
- It has been a while, a long while that I do not have time blogging. It feels good when I put down work and write a blog. In fact, it did not take long to do this coffee table at all. This is my fourth take on...
- The real advantage of gear modelling in 3d is that gears in a mesh do not have to parallel each other. It is posible to demonstrate how gears can transfer rotation (and forces) to orientations other than the...
- The dragon curve is a fractal which is defined by replacing a segment of the curve with a (smaller) version of itself. For better rendering performance, open scene in new window by...