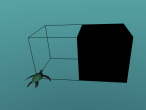
Truncated cube

  • Email
  • Sharebar
  • Email
crystal h's picture
Submitted by crystal h on Wed, 02/04/2014 - 10:11

I have created a truncated cube, I would like to tell you about the truncated cube and how I created it.

Using Wikipedia, truncated cube website I was able to find the following information that I needed to create my shape.

The truncated cube is an Archimedean solid. It has 14 regular faces, 8 equilateral triangles and 6 regular octagons. It has 36 edges and 24 vertices. It is formed by truncating regularly the platonic solid, the cube, as suggested by the shapes name. It has two dihedral angles:

  •     Between the octagonal and octagonal faces: 90° (8-8)
  •     Between triangular and octagonal faces: 125. 264166666666666666666° (3-8)

Using this information and the logo programming tool I was able to create a 3D model of a truncated cube, as seen below.

 

I create this truncated cube by using the following logo programming sequence.

Comments

Andy's picture

14 faces polyhedron

Submitted by Andy on Wed, 02/04/2014 - 11:43.

This is a good looking Archimedean solid and easy to understand that the six corners were chopped off. Thanks for sharing. smiley

I wonder though, the angle a88 was not used, but there is a stange angle 35.264166666666666666666. How did you get this angle? What is it? 

 

crystal h's picture

I found the angle by using

Submitted by crystal h on Wed, 02/04/2014 - 21:45.

I found the angle by using alternating angles to work out that the angle from the outside face of the triangle to a plane parallel to the octagon is also a83. By subtracting 90 degrees we can then use vertically opposite angles to show that the angle of rotation is approximatly 35 degrees. Therefore this angle of rotation is equal to a83 - 90 degrees, which is the angle 35.264166666666666666666. See image below.

 

Andy's picture

Brilliant idea

Submitted by Andy on Tue, 08/04/2014 - 20:32.

This shows great spatial awareness. Thanks for providing visual explanation. cool

Facebook Comments Box