Similar blogs you may be interested in

VAM Temple project

Created by: Andy
Ice Cream Cone

Created by: Andy
3D Graphing

Created by: Andy
Cube to Rectangular Prism

Created by: Jess_G
Truncated...

Created by: advercis
Truncated cube

Created by: crystal h
Fibonacci sequence

Created by: mathskid
A 3D geometric shape

Created by: A974
my world that andy...

Created by: Alex
Amazing shape

Created by: Void Dragon
alienfishspacestation

Created by: stampylongnose
Crazy_2D_Shape

Created by: 135689
Troys first logo

Created by: totta3
my first world

Created by: Random Ness
My First Creation

Created by: TH209
3D Pattern Genorator

Created by: mathskid
floating shape

Created by: Hayley849
bluestar - my first...

Created by: firestar
desert shape

Created by: 12345
Hypercube - Tesseract

Created by: Andy

Author Information

Andy

Offline

Last seen: 17 weeks 4 days ago

Joined: 02/10/2010

Author's blogs

3D Snowflake

29/12/2023 - 22:44:41
Farewell 2021 with 3n+1

31/12/2021 - 13:28:31
Robotic arm

18/01/2020 - 18:26:54
Chaos game - square...

07/12/2019 - 16:43:54
The Sun and Earth model

20/11/2018 - 13:47:49
Hemnes Desk

17/07/2018 - 19:04:28
A pot of green

23/01/2018 - 11:55:15
ATCM 2017 Presentation

17/12/2017 - 13:24:06
Flying boxes

07/06/2017 - 15:17:51
Programming Driven 3D...

04/06/2017 - 16:12:11
Newton's cradle...

05/04/2017 - 17:02:29
Sea simulation

08/03/2017 - 16:09:15
A boat with a sail

08/03/2017 - 15:33:21
Atom Helium

19/07/2016 - 13:26:35
Pokestop

15/07/2016 - 14:42:05

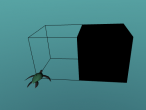
Truncated Icosahedron - Soccer Ball

Submitted by Andy on Sat, 01/03/2014 - 17:01

Quite a few geometry software can produce complicated geometrical objects. The Platonic solids and Archimedian solids for example, can be produced using dynamic geometry systems (DGS). If so, the process would be brilliant but complicated ways of formal Euclidean reasoning. In VRMath2, similar reasoning may be used, but because it has a Logo programming or turtle geometry capability, most of these complicated geometrical solids can actually be constructed by moving locations and turning directions.

In order to construct a soccer ball or a truncated icosahedron using Logo or turtle geometry way, it is necessary to know the distance to move and degrees to turn. Upon reading the information on Wikipedia about truncated icosahedron, I found that all edges are the same length, and there are two useful angles for the construction of this truncated icosahedron. These two angles are the two dihedral angles:

bewteen two hexagonal faces: 138.189685 degrees (6-6)
between hexagonal and pentagonal faces: 142.62 degrees (6-5)

With the above information, I was able to move and turn the turtle in 3D space to construct a soccer ball as below.

The Logo program is as below, but I believe it can be even simpler.

; Truncated Icosahedron (soccer ball)
; By Andy Yeh (2014)
CS RESET
FACE PCOFF
; an effort to have the centre point closer to (0,0,0)
; 2.47801866 is the radius of the circumscribed sphere
RU 90 FD 2.47801866 RD 90
MAKE "a66 138.189685 ; dihedral angle 6-6
MAKE "a65 142.62 ; dihedral angle 6-5
TO hexagon_r SETMAT 5 30 PD REPEAT 6 [FD 1 RT 60] PU END
TO hexagon_l SETMAT 5 30 PD REPEAT 6 [FD 1 LT 60] PU END
TO pentagon_r SETMAT 0 31 PD REPEAT 5 [FD 1 RT 72] PU END
TO pentagon_l SETMAT 0 31 PD REPEAT 5 [FD 1 LT 72] PU END
pentagon_r
REPEAT 5 [
TL 180 - :a65 hexagon_l TR 180 - :a65
FD 1 RT 72
]
REPEAT 5 [
TL 180 - :a65 FD 1 LT 60 FD 1 LT 60 
TR 180 - :a65 pentagon_r TL 180 - :a65
FD 1 LT 60 
TR 180 - :a66 hexagon_r TL 180 - :a66
RT 60 BK 1
RT 60 BK 1 RT 60 BK 1 TR 180 - :a65
FD 1 RT 72
]
REPEAT 5 [
TL 180 - :a65 FD 1 LT 60 FD 1 LT 60 FD 1
TR 180 - :a65 RT 72 FD 1 RT 72
TL 180 - :a65 hexagon_l
FD 1 LT 60 FD 1 LT 60
TR 180 - :a65 pentagon_r TL 180 - :a65
RT 60 BK 1 RT 60 BK 1
TR 180 - :a65
LT 72 BK 1 LT 72 TL 180 - :a65
BK 1 RT 60 BK 1 RT 60 BK 1 TR 180 - :a65
FD 1 RT 72
]
REPEAT 5 [
TL 180 - :a65 FD 1 LT 60 FD 1 LT 60 FD 1
TR 180 - :a65 RT 72 FD 1 RT 72
TL 180 - :a65 FD 1 LT 60 FD 1 LT 60 FD 1 LT 60
TR 180 - :a66 hexagon_r TL 180 - :a66
RT 60 BK 1 RT 60 BK 1 RT 60 BK 1 TR 180 - :a65
LT 72 BK 1 LT 72 TL 180 - :a65
BK 1 RT 60 BK 1 RT 60 BK 1 TR 180 - :a65
FD 1 RT 72
]
TL 180 - :a65 FD 1 LT 60 FD 1 LT 60 FD 1
TR 180 - :a65 RT 72 FD 1 RT 72
TL 180 - :a65 FD 1 LT 60 FD 1 LT 60 FD 1 LT 60
TR 180 - :a66 FD 1 RT 60 FD 1 RT 60 FD 1 RT 60
TL 180 - :a65 pentagon_l