Farewell 2021 with 3n+1

The Youtube algorithm one day pushed a video "The Simplest Math Problem No One Can Solve - Collatz Conjecture" to me. After viewing the video, I thought that my VRMath2 could easily visualise the 3n+1 graph with its LOGO programing. I am happy that my VRMath2 application is still working after almost three years in low maintenance mode. With some simple coding. I have written a LOGO program that can take a number (natural number) and the turtle will draw its 3n+1 graph. The 3n+1 problem is simple. It starts with a natural number; if the number is odd, multiply it by 3 then add one; if the number is even, the number is divided by 2. These rules apply until the resulting number is one. It is interesting that it seems any given natural number will end with 1 after applying the 3n+1 rules, but how?

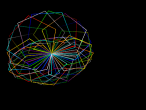
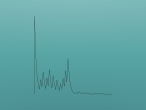
Below is the graph for the number 2021 (the date when this blog is wriiten is 31-12-2021), so to farewell 2021.

The LOGO codes are explained below:

; 3n+1 conjecture graph
; By Andy Yeh (2021)
CS CT RESET
; sub routine checking if a number is odd or even
TO isOdd :num
  IFELSE BITAND 1 :num [ OUTPUT TRUE ] [ OUTPUT FALSE ]
END
; read a number from keyboard (user input)
MAKE "n (READWORD [Entre a whole number (n)?])
; make sure the input number is a natural number
IF NOT (NUMBER? :n) [ PRINT [Please enter a whole number that is greater than 1] BYE ]
IF :n < 2 [ PRINT [Please enter a whole number that is greater than 1] BYE ]
MAKE "n ROUND :n
(PRINT [ Number FOR graphing is ] :n)
; start turtle graphing
MAKE "step 0  ; record number of steps
MAKE "max 0   ; record maximum number in the number sequence
PD
WHILE (:n > 1) [
  IFELSE isOdd :n
  [ MAKE "n :n*3+1 ]
  [ MAKE "n :n/2 ]
  SETXYZ :step :n 0
  MAKE "step :step + 1
  IF :n > :max [ MAKE "max :n ]
  PRINT :n
]
PU
; report results in the console
(PRINT [Number of steps: ] :step)
(PRINT [Max number: ] :max)
; scale the graph by the ration of max/step for better looking
SELECT OBJECT
SETSX :max / :step
SHOWALL ; fit the graph into the 3D screen

The logic or the 3n+1 rules are coded from line 19 to 27.  Within this WHILE loop, the SETXYZ will move the turtle to the coordinate, which has the n as the Y coordinate, the step as the X coordinate, and alway 0 as the Z coordinate. I have also recorded a short video below showing how you could try it for yourself. 

The 3n + 1 conjecture predicts that no matter which positive integer is given, the number sequence will eventually reach 1. In trying the 3n + 1 program in VRMath2 Editor, I have also developed some questions for further investigation:

• Would the bigger number have longer sequence?
• Would every number have different number of step? 
• Can you find 3 numbers that will have the same number of steps in their sequences?
• What number will keep being even when divided by 2, all the way to 1?
• What is special about 3n+1? Why not 2n+1 or 4n+1 or 3n+3?
• What other ways can the number sequence be visualised?

Please leave a comment to let me know what you think.

Files: 3n_plus_1.x3d | 3n_plus_1.logo