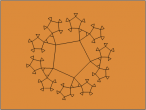
Cayley graph 3D

I was in the keynote session of AAMT conference. In the keynote, the mathematician Hanna Neumann was mentioned. I immediately googled and started reading about her on Wikipedia.

While reading, my thoughts are like the hyperlinks that go everywhere, then suddenly I saw and clicked into the Group theory, where I found the Cayley graph that caught my attention.

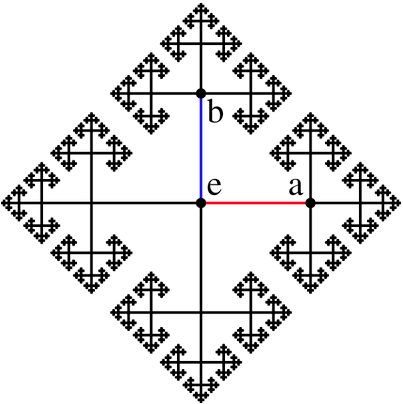
It is easily recognisable that this cayley graph is a fractal image, which can be produced with a simple recursive procedure in VRMath2's LOGO language.

The graph has four identical branches. Therefore, we only need to analyse one branch then when it is done, we can rotate the turtle to make other three branches.

Let's look at the top branch that starts from e to b.  From e to b, we forward the full length, then it splits into three branches with the length reduced in half.

With this rule in mind, I then wrote the following procedure:

; Recursive procedure for Cayley graph
;
TO cayley :size
IF :size < 5 [ STOP]
FD :size
LT 90 cayley :size * 0.5 RT 90
cayley :size * 0.5
RT 90 cayley :size * 0.5 LT 90
JB :size
END
;
CLEAN ; clear objects in space
HOME ; go to home position and orientation
CM ; centimeter as unit of measurement
LINE ; record turtle track as line
PD RU 90
REPEAT 4 [cayley 100 RT 90]
PU
;

Then I came up with an idea to make it a 3D fractal image. If I insert a scaled cube after every forward, what would it be like? It turned out to be quite nice actually with 3 more lines of code (lines 5-7).

; Recursive procedure for Cayley 3D graph
TO cayley :size
IF :size < 5 [ STOP]
FD :size
MAKE "scale :size/180  ; make a variable :scale with value :size/180
SETSCALE :scale :scale :scale  
BOX ; a scaled box
LT 90 cayley :size * 0.5 RT 90
cayley :size * 0.5
RT 90 cayley :size * 0.5 LT 90
JB :size
END ; end of procedure
CLEAN
HOME
CM
LINE
PD RU 90
REPEAT 4 [cayley 100 RT 90]
PU

Please leave a comment and let me know what you think. :-)