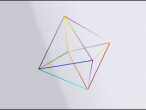
My first Icosahedron
Icosahedron is the last of the five Platonic solids. It consists of 20 regular triangular faces.
I am sure that there is a more efficient way to do this...
How to get 31.71747441146....
I approached this problem from a geometry perspective,
when considering the icosahedron, I first decided that I wanted to create a regular solid. After much trial and error, I discovered that the easiest way to approach this problem was to consider the turtle at the top of one of the points, I then needed to work out the angle of depreciation if the the turtle was to move along one of the edges.
By imagining that the top of the icosahedron was cut off, I had a regular pentagonal based pyramid, from this, I needed the angle from the base to the top along one of the edges. (see below)
I used the length for each side of the icosahedron as being 2 (the edges going to the point in the above image.
What was needed: knowledge of RAT trigonometry
I planed to used the cosine ratio - cos(x) = adjacent/hypotenuse
the hypotenuse is given as 2, so I needed to work out the adjacent (b)
to do this, I looked at the isoceles triangle created in the pentagon when joining the center to two adjacent corners. (see below)
again, using the cosine ratio: cos(x)=adjacent/hypotenuse, hence, cos(54)=1/b, hence: b=1/cos(54)
from here, I can now go back to my original equation
cos(x) = adjacent/hypotenuse
cos(x) = b/hypotenuse
cos(x) = 1/cos(54)/2
x=cos-1(1/(2cos(54)))
x=31.71747
- Knoblauch's blog
- Login or register to post comments
- 9483 reads

























Comments
Strange angle
Hi Knoblauch,
How did you work out the angle 31.71747441146?
Andy :-)