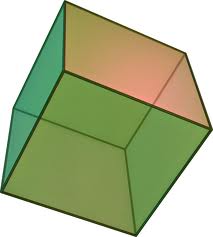
Hexahedron
Introduction
Platonic solids are polyhedron which satisfy 3 conditions
- all its faces are congruent convex regular polygons,
- none of its faces intersect except at their edges, and
- the same number of faces meet at each of its vertices
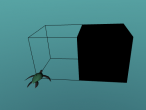
Hexahedron
The most commonly recognised platonic solid, also known as a cube.
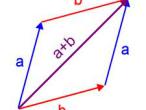
- A hexahedron consists of 6 congruent square faces (satisfying condition 1)
- Each vertex consists of the meeting of 3 faces (satisfying condition 3)
Creation
There are several techniques to create the hexahedron, this first hexahedron shows the edges and vertices, but not the solid faces. Of the various techniques used, this is possibly the easiest.
- Begin with a square - forward 1 unit turn right 90 degrees, repeat 4 times.
- Next, consider how the cube is formed, at each corner of our original square, we need to go up 1 unit - up 1 then down 1 to return to the base square, repeated at each corner
- Finally, to create the top, go up 1 unit at one of the corners then create a new square
this is summarised in the logo code below
In order to show the faces, the procedure required becomes more complex, as each of the 6 faces will need to be completed individually, however the same basic principle applies
Resources
Logo instructions for the two hexahedrons:
cube.logo (outline version)
cube_solid.logo (solid version)
- Knoblauch's blog
- Login or register to post comments
- 12745 reads