Vectors in 3 Dimensions
Vectors in 3 Dimensions
Mathematical background
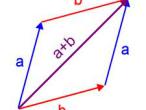
In mathematics a vector has a magnitude (length) and direction expressed as an ordered list of tuples (x, y, z). It is sketched as a directed line segment (arrow). Unless otherwise given, a vector does not impart information about location (when studying in secondary education, we use the origin (0,0,0) of a set of axis as the initial point of a vector.
Unit vectors
i in the direction of the x-axis
j in the direction of the y-axis
k in the direction of the z-axis
a vector is written in the form ai + bj + ck
where a, b and c represent the distance from the origin (0,0,0)
hence 2i + 3j - 1k would be
- 2 units along the x-axis – this can be achieved using the command EAST
- 3 units up the y-axis– this can be achieved using the command UP
- 1 unit forward along the z-axis– this can be achieved using the command SOUTH
To show the vector 2i +3j -1k
we need to move east 2, up 3 and north -1
to show the final vector only we can set the final position – MAKE “A POS
return to home, then use the command sequence
LINE PD SETPOS “A PU
Full code
File: basic_vector.x3d
note: use the command LABEL POS to show the current position
We can then make this into a more generic code
We can now create any vector
This is a very simplistic way to show our vector. As we explore more complex questions we need to alter our processes.
- Knoblauch's blog
- Login or register to post comments
- 5529 reads