I was in the keynote session of AAMT conference. In the keynote, the mathematician Hanna Neumann was mentioned. I immediately googled and started reading about her on Wikipedia.
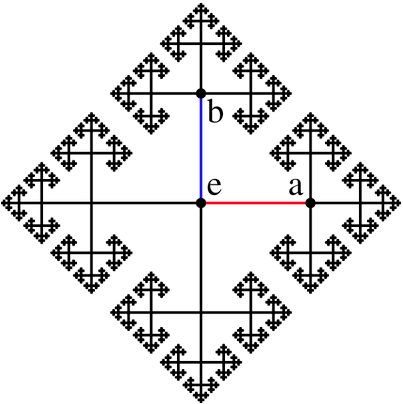
While reading, my thoughts are like the hyperlinks that go everywhere, then suddenly I saw and clicked into the Group theory, where I found the Cayley graph that caught my attention.
It is easily recognisable that this cayley graph is a fractal image, which can be produced with a simple recursive procedure in VRMath2's LOGO language.