Tetrahedron

The tetrahedron has the smallest number of faces in the five Platonic Solids, having only 4 faces. And in fact, four faces are the minimium requirement for a polyhedron. Other features of tetrahedron includes:

• Each face is an equilaterial triangle
• Each vertex is the meeting of 3 faces

Creation

There are 2 main ways to create a tetrahedron - using trigonometry to consider the angle between faces, or, from using a hexahedron (cube) as a base.

Using trigonometry

A tetrahedron is made from 4 equilateral triangles, hence, to start, we need a process to create an equilateral triangle. Previous experimentation has revealed that a simple code will create an equilateral triangle.

For our purposes, I have expanded this code to:

FD 1 MAKE "CA POS FD 1 RT 120 MAKE "A POS
FD 1 MAKE "AB POS FD 1 RT 120 MAKE "B POS
FD 1 MAKE "BC POS FD 1 RT 120 MAKE "C POS

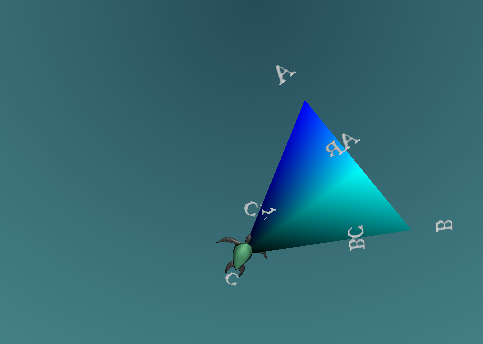This allows reference points at each vertex, and the midpoint of each side to be used in future instructions.

The next step in creating our tetrahedron is to create another equilateral triangle, with a common side to the existing triangle. Before we can place this triangle however, we need to determine the angle at which these two faces should meet (hence the idea of needing trigonometry in the creation)

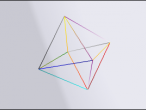
To determine the dihedral angle (angle between the faces), consider the diagram right. we need to determine the angle of XYZ, to do this, we need to determine the size of side XY and YZ (the side XZ is equal to the sides of the equilateral triangle) XY and YZ are both equal, and can be found by determining the size of AB to C from our initial triangle (see diagram 2) using Pythagoras, we can determine that the length of XY is equal to.

If we let the length of one side equal to x, then the distance A to AC is x/2, we need to find the length of AC to B (this will become XY).

using the cosine rule, we can determine that the angle XYZ is 70.528779

Now that we have this angle, we can align our turtle by using the command RU 70.528779, the rest of the code, then positions the turtle at the vertex, allowing the use of our previous equilateral triangle code

PU
SETPOS :CA TOWARDS :B
RU 70.528779 LT 90 FD 1
PD
RT 120 FD 2 RT 120 FD 2 RT 120 FD 2

This is repeated 3 times, changing the initial position for each side. The final product is shown here.

Using a cube

A non-algebraic method to create a tetrahedron is to begin with a cube (instructions for the construction a cube can be found in the post on hexahedrons)
We know that a tetrahedron is made from equilateral triangles, so we need to consider how to create an equilateral triangle within our cube.

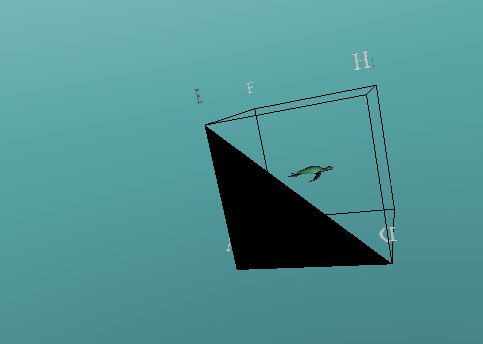If we consider vertex A to be part of our first equilateral triangle, we have options to connect this to either B, D or E along edges of the cube.  These options will create isosceles triangles, not equilateral. 

Another option would be to connect A to G, however, this would go through the centre of our cube, and is not appropriate.

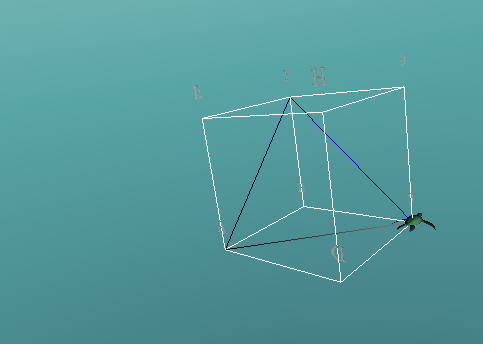
The next logical option would be to connect to either C, F or H, this would create a side diagonally across one of the faces. If we were to use 2 of these options, for example, connect AC and AF, to complete a triangle, we would connect CF, which is also the diagonal distance across a face of the cube, hence creating an equilateral triangle.

Repeating this process we connect the vertices A, H, C and F.

FACE
SETPOS :A PD SETPOS :C SETPOS :F PU
SETPOS :A PD SETPOS :C SETPOS :H PU
SETPOS :F PD SETPOS :H SETPOS :C PU
SETPOS :A PD SETPOS :H SETPOS :F PU