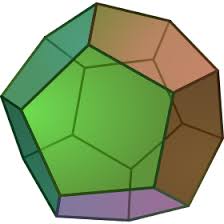
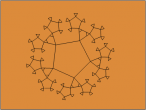
Dodecahedron
Dodecahedron is one of the five Platonic Solids. It consists of
- 12 faces (congruent pentagons)
- 30 edges
- 20 vertices (the meeting of 3 faces)
Construction
From Trigonometry
A basic pentagon can be created from the basic code
note: the internal angle of a regular pentagon is 108o, making the external angle, which we are are turning, 72o
from this initial pentagon, we need to create pentagons connecting to our 5 initial edges. To do this, we need to consider what angle these are to be connected at. The dihedral angle of a dodecahedron is116.56505° = arccos(-1/√5), meaning that we need to tilt down 63.43495o
this process needs to be repeated several times to create all edges of our dodecahedron. The final code would look something like.
- Knoblauch's blog
- Login or register to post comments
- 18122 reads
























Comments
Its quite difficult to do it
Its quite difficult to do it , Still not able to get the concept clearly.
start small
By the time I attempted the dodecahedron, I had already worked my way through the simpler platonic solids. This allowed me to familiarise myself with the coding whilst creating solids which I found easy to understand. There were still a lot of false starts and editing before I succesfuly completed the dodecahedron.